Основные приемы анализа при картографическом методе исследования

Сама суть географических карт как математически определенных пространственных моделей предопределяет эффективность математических приемов их -анализа для получения новых характеристик отображенных на картах явлений, для изучения их взаимосвязей и зависимостей, для построения математических моделей и других целей.

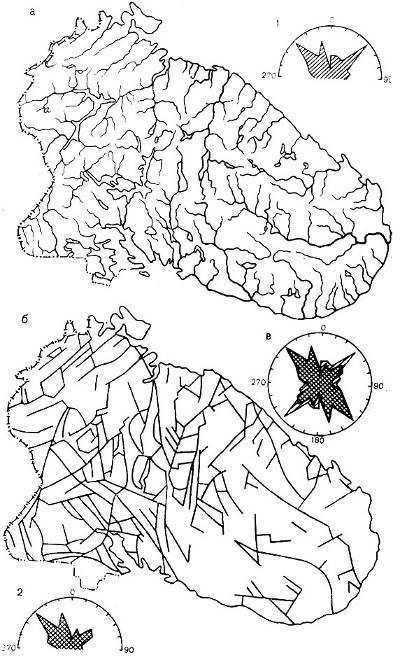
Рис. 6. Графический анализ взаимосвязи гидрографической сети Кольского п-ова с линиями неотектонических разломов: а - карта речной сети и диаграмма ориентирования рек по основным направлениям горизонта; б - карта неотектонических нарушений и соответствующая диаграмма; в - совмещение диаграмм: 1 - речной сети; 2 - неотектонических нарушений

Очень популярен математико-статистический анализ, привлекаемый к исследованию явлений, которые можно рассматривать на картах как однородные множества изменяющихся в пространстве случайных величин: высот, температур, посевных площадей, урожайности и т. п., называемых в математической статистике статистическими совокупностями. Среди многих задач, решаемых по картам при помощи статистического анализа, можно выделить три основные: 1) определение статистических характеристик какого-либо однородного явления, зависящего от многих факторов с неизвестной функциональной связью; 2) изучение пространственных и временных связей между явлениями; 3) оценка степени влияния отдельных факторов на изучаемое явление и выделение ведущих факторов.

Для характеристики явления посредством какого-либо статистического показателя (средней арифметической, моды, медианы и т. п.) определяют количественные значения явления во многих точках карты и обрабатывают полученные данные, следуя правилам математической статистики по ячейкам избранной территориальной сетки (административного деления, природного районирования, регулярной сети и т. п.). Для производства выборки наиболее удобны карты с изолиниями (или псевдоизолиниями), позволяющими определять величину явлений в любой точке карты. Наиболее обоснована выборка по сетке равномерно расположенных точек. Количественные значения для статистической обработки можно получать и по картам с другими способами изображения: точками, ареалами, картограммами. Например, при точечном способе определяют интенсивность явлений выборочно по сетке контрольных площадок (часто в виде кружков), подсчитывая число точек внутри каждой контрольной площадки. Обычно анализ завершают построением картограммы или изолиний (псевдоизолиний), дающих наглядное представление о пространственных изменения показателя.

При исследовании по картам пространственных (и временных) зависимостей явлений - их формы и тесноты - прибегают к вычислению корреляционных показателей (коэффициентов корреляции, корреляционных отношений, показателей множественной корреляции и др.) и к выяснению (оценке) их надежности. Для этого надо иметь две выборки значений сопоставляемых явлений (например, осадков и урожайности), измеренных в одних и тех же точках одной или двух сравнимых карт; для множественной корреляции привлекают три выборки и более по одной или нескольким картам. Такие исследования при детализации расчетов по сетке территориального деления дают материал для составления карт взаимосвязей (корреляций), показывающих пространственные изменения величины и знака показателей корреляции; по ним возможно районирование территории по характеру связей - тесных и слабых, положительных и отрицательных, что важно для установления причинно-следственных отношений между исследуемыми явлениями. Картографостатистическое изучение взаимосвязей теперь широко используется не только в географических исследованиях, то также в других отраслях знания, в частности в геологии, метеорологии и медицине.

Задачи по оценке влияния отдельных факторов и выделению ведущих факторов возникают при исследовании по картам сложных комплексов явлений со множеством взаимосвязей. Примерами могут быть совокупность климатических показателей, или, что значительно шире, комплекс природных условий. Математическая статистика предоставляет для этого средство в виде факторного анализа, который позволяет сводить в одном показателе (аппроксимировать одним фактором) влияние комплекса родственных явлений и в конечном счете обобщать и оценивать влияние многих факторов при помощи весьма ограниченного числа синтетических показателей. Такой путь исследования дает объективное средство к составлению синтетических карт, например комфортности природных условий для обитания и работы людей.

Это интересно:

Загрязнение гидросферы
С водой ситуация хуже: сброс загрязненных сточных вод в ЮФО составил 2,439 млрд кубометров, то есть вырос почти на 8%. Наибольший "вклад" внесли Краснодарский край, где сосредоточено 80% от общих эксплуатационных ресурсов пресных вод Северо-Кавказского региона, Ингушетия и Калмыкия. По д ...

Климатообразующие факторы
Выделяют три главных климатообразующих фактора и факторы, влияющие на климат. Главные факторы - это факторы, определяющие климат в любой точке земного шара. К ним относятся: солнечная радиация, циркуляция атмосферы и рельеф местности. Солнечная радиация - фактор, определяющий поступление солнечно ...

Физико-географическое районирование территории Кыргызстана
Большие абсолютные высоты, сложное геологическое и орографическое строение Киргизии, её географич. положение в глубине Евразиатского материка, в окружении обширных пустынь и связанная с ними континентальность и засушливость климата, создают большую пестроту ландшафтов, разнообразие природных услов ...