Построение цифровой модели рельефа. Общие сведения о цифровых моделях рельефа

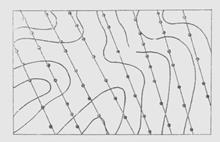
Рисунок 8-Расположение точек на линиях профиля в частично регулярной модели

Измеряемые точки могут располагаться на горизонталях с равным и неравным шагом.

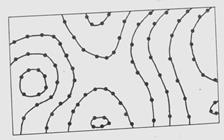
Рисунок 9-Расположение точек на горизонталях в частично регулярной модели

Рассмотрим один из вариантов формирования функциональной ЦМР на примере построения модели профиля рельефа.

Построение цифровой модели профиля рельефа. Для построения функциональной модели профиля рельефа можно использовать различные алгоритмы, в данном случае для формирования ЦМР предлагается сплайн-аппроксимация, сущность метода сводится к следующему.

Функция рельефа f(У) на отрезке [а,b] задается координатами Уi, Zi;. точек, т.е. дискретно.

Рисунок 10-Профиль рельефа

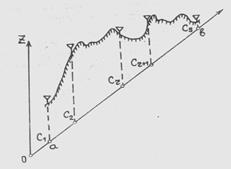
Рисунок 11-Разбивка профиля на элементарные отрезки

Перед аппроксимацией рельефа данным методом строится промежуточная модель. Для этого вычисляются отметки всех граничных точек элементарных участков _[Сг , Сг+1] профиля и стандартных точек с координатами Yn. (n=I,….,5) на каждом элементарном участке. [1]

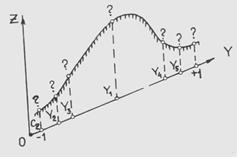
Рисунок 12-Разбивка профиля на элементарные отрезки

Элементарный отрезок [Сг , Сг+1] со стандартными точками Yn (n=I, 5).

Значения функции рельефа f (Уn) в указанных точках находятся путем линейной интерполяции по измеренным точкам. Для этого относительно каждой определяемой точки “n” ищутся два ближайших исходных пикета, расположенных слева и справа от точки " n " .

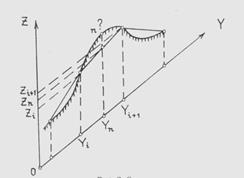
Рисунок 13-Графическая интерпретация линейной интерполяции

Вычисление искомой отметки в точке с координатой Yn, выполняется по формуле (4)

(4)

Где Yn , Yn+1 - плановые координаты исходных точек, ближайших к определяемой;

Yn - координата определяемой точки; Zn - отметка определяемой точки;

Zi , Zi+1- измеренные отметки исходных точек.

Конечным результатом построения ЦМР являются коэффициенты Bi полиномов вида на каждом элементарном участке [Cr,Cr+1] которые находятся по способу наименьших квадратов при условии непрерывности на границах элементарных отрезков [ Сr ,Сг+1].

(5)

Точность построения ЦМР зависит от плотности точек исходной информации, размера элементарного участка аппроксимации и сложности (расчлененности) рельефа. Необходимо помнить, что на каждом элементарном участке [Сr , Сг+1] аппроксимации должно быть не более двух точек экстремума функции рельефа. За точки экстремума функцииZmin. и Zmax принимаются такие между которыми уже нет других точек перегибов рельефа требующих отображения.

Это интересно:

Газоперерабатывающая промышленность
В отличие от нефти, природный газ не требует большой предварительной переработки для использования, но его необходимо сразу, отправлять к потребителю. Газ — главный вид топлива там, где нет других энергетических ресурсов. Он используется в промышленности (80%) — электроэнергетика, химия, металлург ...

Факторы размещения производительных сил
В зависимости от различных элементов, воздействующих на развитие региона, можно выделить следующие группы факторов: природно-географические, экономические, технико-технологические, социодемографические, политико-правовые. В рамках перечисленных групп в соответствии со сферой действия все факторы д ...

Применение фотограмметрии в архитектуре
Все строительные сооружения постоянно подвергаются разрушительному воздействию сил природы и цивилизации и поэтому требуют ремонта через определенные промежутки времени. Если при этом речь идет о памятниках архитектуры, то необходимые работы нужно подготавливать с особой тщательностью и производит ...